Fábula matemática

"Três amigoss almoçaram num restaurante e cada um entregou ao empregado uma nota de 10 euros, perfazendo um total de 30, para pagar a conta. O empregado entregou o dinheiro ao caixa, que devolveu 5, pois a conta era de 25. Como os clientes não sabiam o valor da conta, o empregado resolveu enganá-los. Guardou 2 euros e entregou 1 de troco a cada cliente. Assim, cada cliente pagou 9, num total de 3 x 9 = 27, que somados aos 2 que ficaram com o empregado dão um total de 29. Como explicar o misterioso desaparecimento de 1 euro?"

Enigma da lua - resposta.

Prova-se que os triângulos [DEC] e [EAC] são semelhantes. Da proporcionalidade entre as medidas dos lados dos triângulos conclui-se que:
(r-5)(r-5)=r(r-9).
Assim r = 25 e as medidas dos diâmetros são 50 e 41 polegadas.

E o professor, como fica?

O professor que se formou em um tipo de matemática e depois não teve oportunidade de se aperfeiçoar, discutir visões metodológicas distintas, reproduz com seus alunos o que aprendeu porque acredita que deva ser daquele jeito. Há uma geração de professores sem referencial para refletir, que não acredita que poderia ser de outro modo. Ele aprendeu divisão de polinômios na sétima série, e acha que deve ensinar polinômios na sétima série. Muitas vezes não sabe que existem investigações sérias sobre desenvolvimento do pensamento algébrico, que mostram que certas operações com polinômios são inadequados nessa fase, precoces etc. Faz falta o conhecimento da história do currículo para compreender que as mudanças são necessárias. É preciso conhecer os livros antigos de matemática, acompanhar as mudanças para poder fazer uma crítica daquilo que vamos chamar de ensino tradicional. Trata-se de uma prática que tem características muito específicas muitas vezes inadequadas para a formação do indivíduo de hoje.

Qual é a grande questão do ensino da Matemática hoje?

É fazer com que se tenha a Matemática para todos. A exclusão provocada pela Matemática, a Matemática em relação a outros segmentos sociais, Matemática e gênero. Hoje, discute-se, pesquisa-se isso seriamente. Todos os indivíduos sãos têm condições plenas de pensar matematicamente, enfrentar situações de matemática complexa. O que não quer dizer que tenham que se tornar craques em matemática. Todo indivíduo pode acessar uma matemática que vai além das quatro contas.

A beleza da matemática

1 x 8 + 1 = 9
12 x 8 + 2 = 98
123 x 8 + 3 = 987
1234 x 8 + 4 = 9876
12345 x 8 + 5 = 98765
123456 x 8 + 6 = 987654
1234567 x 8 + 7 = 9876543
12345678 x 8 + 8 = 98765432
123456789 x 8 + 9 = 987654321

1 x 9 + 2 = 11
12 x 9 + 3 = 111
123 x 9 + 4 = 1111
1234 x 9 + 5 = 11111
12345 x 9 + 6 = 111111
123456 x 9 + 7 = 1111111
1234567 x 9 + 8 = 11111111
12345678 x 9 + 9 = 111111111
123456789 x 9 +10= 1111111111

9 x 9 + 7 = 88
98 x 9 + 6 = 888
987 x 9 + 5 = 8888
9876 x 9 + 4 = 88888
98765 x 9 + 3 = 888888
987654 x 9 + 2 = 8888888
9876543 x 9 + 1 = 88888888
98765432 x 9 + 0 = 888888888

Brilhante, não é?

E que tal esta simetria:

1 x 1 = 1
11 x 11 = 121
111 x 111 = 12321
1111 x 1111 = 1234321
11111 x 11111 = 123454321
111111 x 111111 = 12345654321
1111111 x 1111111 = 1234567654321
11111111 x 11111111 = 123456787654321
111111111 x 111111111 = 12345678987654321

Matemática!7x13=28?

Matemática

 

Momentos

Cheguei ao quadro e peguei no giz
Do nosso amor fiz uma equação.
Andei depois às voltas com o X,
Do teu desconhecido coração.

Desejava somente conhecer
O valor da incógnita querida,
P’ra que então pudesse resolver
O problema maior da minha vida.

Da fórmula geral do nosso afecto,
Comecei a fazer deduções…
E – podes crer – meu fito predilecto,
Era igualar as nossas afeições.

Queria reduzir à unidade
As nossas almas, porque os meus intentos,
Eram apenas pôr em igualdade
As expressões dos nossos sentimentos.

Mas, ao chegar às deduções finais,
Eu pude ver então, nesse comenos
Que o meu afecto tinha o sinal +
E o teu, formosa ingrata, o sinal -.


Júlio Dias Nogueira (1939)

O poema matemático de Juliano

Cansado de sentir os solavancos da vida
Juliano, homem de porte romano, comprou uma calculadora.
Gastou um pouco do economizado numa máquina belga
que fazia todas as contas que Juliano não precisava fazer.

Calculou todos os gastos,
as incertezas,
as dúvidas,
as incoerências,
os prejuízos,
e os desencontros.

Em contrapartida, Juliano somou as alegrias,
as chegadas,
os festivais,
sorvete de Flocos,
gemidos de gozo
e lágrimas de êxtase.

Juliano era mesmo sabido com sua calculadora belga.

Na prova dos nove, encontrou resultado de dígito negativo;
Juliano era mesmo sabido
e a matemática recomendou
que ele desse cabo na própria vida.

Com seu porte romano, Juliano esqueceu da fortuna belga
e aquietou-se nos apoios da janela.
A matemática e a poesia, pensou,
e num súbito impulso saltou para dentro de um livro
virando personagem de ficção.

Esperto, Juliano transformou a sua dor em best-seller
e a calculadora belga em artigo de coleccionador.

Vale apena aprender matemática

Para muitos a Matemática é um problema
Mas não é bem assim
Aprendê-la vale a pena.
Observem que em tudo ela está presente
É nossa aliada
E faz bem pra toda gente.
Somar, subtrair 
Quero aprender.
Multiplicar e dividir
Quero aprender.
Porcentagem e fração
Quero aprender
A Matemática é nossa amiga
Vamos todos conhecer.

 

Maria Sandra Andrade Santos

matemática desafia os estudantes

A matemática sempre foi o grande bicho papão de boa parte dos estudantes. Tanto que no Exame Nacional do Ensino Médio (Enem), é justamente nesta disciplina que os candidatos tem um desempenho abaixo das demais matérias que fazem integram o caderno de provas.

Dificuldade começa nos primeiros anos escolares | Foto: Reprodução internet

Muitos especialistas  se surpreendem com o resultado, pois consideram os textos de Matemática mais simples e objetivos em comparação as demais matérias. Para o professor André Junger, do curso Pré-militar Virtual, a explicação está na forma como ela é ensinada.
"Essa dificuldade já começa nos primeiros anos escolares, quando os alunos não conseguem ver beleza e nem aplicabilidade na matemática. Isso acontece porque os professores se preocupam em ensinar só a teoria, dissociada da parte recreativa e curiosa da disciplina. Se o aluno não consegue visualizar a ligação com a prática, do que é ensinado, ele perde totalmente o interesse", explica o educador.
Segundo Junger, caberia a escola incentivar o professor a abandonar o método  tradicional. " O aluno acaba desempenhando um papel quase sempre passivo. A escola deve procurar estabelecer um diálogo com os alunos, estimulando a imaginação, de modo a conduzi-los à redescoberta", destaca.
 Matheus Rodrigues, 16 anos, aluno de uma escola particular na Zona Sul do Rio, assume que seu desempenho nesta disciplina é apenas razoável. A saída encontrada por seus pais, para evitar a reprovação, foi recorrer a uma explicadora.
"Desde pequeno a Matemática foi minha maior inimiga na escola. Posso passar horas estudando e no final, aprendo o suficiente para não tirar nota baixa. Confesso que estou preocupado quando chegar a hora de enfrentar o Enem, pois espero ter problemas nesta matéria", afirma.
Se para muitos estudantes a Matemática é um fantasma, ela não assusta Cristina Moreira, 17 anos. "Não posso dizer que seja a minha matéria preferida na escola, gosto mais de História e Geografia, mas consigo tirar boas notas. Claro que tenho que dedicar mais tempo do que destino as outras matérias. Talvez não tenha tanta dificuldade, como acontece com vários colegas de sala, porque tive professores que me ajudaram bastante", revela.
Contas
Faltando pouco mais de 20 dias para as provas do Enem, a maioria dos estudantes começa a intensificar o estudo, tentando ter um desempenho, pelo menos razoável, no exame. Segundo André Junger, este não é o melhor método.
"O ideal não é estudar faltando cerca de um mês para o exame, porém com a falta de tempo, a saída é a resolução das questões de provas anteriores. O aluno deve investir mais na interpretação das questões, bem como o domínio de desenhos geométricos", orienta o professor.

passeios pela matemática

Embora invisível a Matemática ocupa um papel cada vez mais significativo no nosso dia-a-dia.

Se não houvesse Matemática não existiriam...

• edifícios
• pontes
• linhas eléctricas
• cabos de telefone
• aviões
• computadores
• microondas
• automóveis
• pacemakers
• …

Com a Matemática é possível explicar diversos fenómenos do dia-a-dia.

Fenómeno	Explicação matemática
Como é que um avião se mantém no ar sem algo a suportá-lo?	Equações descobertas por Daniel Bernoulli no século XVIII
O que faz com que uma maçã caia de uma árvore na terra? O que mantém a Terra a girar em torno do Sol?	Equações do movimento e da mecânica descobertas por Newton no século XVII
Como é que as imagens e sons de um jogo de futebol aparecem numa TV em qualquer parte do mundo?	Através da radiação electromagnética descrita pelas equações de Maxwell, século XIX
Sons musicais	Foram estudados por Aristóteles
A Terra é circular	2000 anos antes de enviarmos uma nave espacial para o espaço que nos fornece fotografias da Terra, Eratóstenes usou a Matemática para provar que a Terra é circular. Calculou o seu diâmetro e a sua curvatura com 99% de exactidão.
Quem vai ganhar nas eleições?	Previsão com base na teoria das probabilidades e estatística
Amanhã vai chover?	Previsão com base no cálculo
Estudo do comportamento do mercado de valores de uma bolsa	É feito pelos analistas de mercado com várias teorias matemáticas.
Qual o valor do seguro de vida a pagar?	As companhias de seguros usam estatística e probabilidades para ajustarem os seus prémios de acordo com a probabilidade de se ter um acidente durante o ano.

você sabe o que são números triangulares?

Os primeiros números triangulares são 1, 3 e 6. Veja por que:

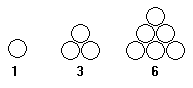
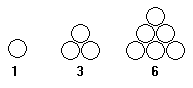
Os números triângulares podem ser calculados através de duas fórmulas: a iterativa e a recursiva:

Fórmula iterativa
T(n) = 1+2+3+...+n

Fórmula recursiva
T(1) = 1
T(n+1) = T(n)+(n+1)