Qual é o próximo número desta sequência ?

4 8 16 32 ....

Conflito entre ateus e cristãos

A zoo lógica

Na época em que os bichos falavam, numa floresta viviam dona Onça e dona Hiena, comadres inseparáveis, com características peculiares. Dona Hiena mente às segundas, terças e quartas-feiras: dona Onça mente às quintas, sextas e sábados. Nos dias que não mentem, elas dizem a verdade.

Certa vez, num encontro, dona Hiena e dona Onça conversaram:

- Olá, dona Onça ! Ontem eu menti - disse a dona Hiena.

- Olá, dona Hiena ! Eu também menti ontem - retrucou dona Onça.

Em que dia aconteceu esse encontro ?

Você sabia?

    Que o maior número primo conhecido é , que tem 2.098.960 dígitos e foi descoberto em 01/06/1999 por Nayan Hafratwala, um participante do GIMPS, um projeto cooperativo para procurar primos de mersenne.

    Que são conhecidos 51539600000 casas decimais de (Pi), calculadas por Y. Kamada e D. Takahashi, da Universidade de Tokio em 1997? E que em 21/08/1998 foi calculada pelo projeto Pihex a 5000000000000^a. casa binária de (Pi).

O número considerado mágico

Curiosidade Matemática #9 – 1089: O Número (dito) Mágico

A razão para que o número 1089 seja considerado “mágico” decorre do fato de ser obtido da seguinte forma:

Dado um número qualquer composto de três algarismos diferentes – abc -, inverta esse número, no sentido de trás para frente – cba – e subtraia o menor do maior. Ao resultado dessa subtração – representada por xyz -, onde se deve considerar sempre um número de três algarismos, mesmo quando a diferença na casa das centenas é zero, some o seu inverso – zyx – e eis que surge “fagueiro” o número 1089.

O objetivo deste post é demonstrar porque isso sempre ocorre. Mas, antes alguns exemplos para que não restem eventuais dúvidas quanto ao enunciado.
Exemplo 1: Seja 367 um número escolhido, que escrito de trás para frente é 763. Subtraindo o menor do maior obtemos:

763 – 367 = 396

E somando o resultado obtido ao seu inverso de trás para frente:

396 + 693 = 1089

Exemplo 2: Agora tome o número 675. Utilizando-se dos mesmos procedimentos vem:

675 – 576 = 099 => 099 + 990 = 1089

Observe que no exemplo acima o zero a esquerda – em 099 – deve ser considerado para que o resultado seja o número “mágico” 1089.

Multiplicação ( . ) e divisão ( :

    O sinal de X, como que indicamos a multiplicação, é relativamente moderno. O matemático inglês Guilherme Oughtred empregou-o pela primeira vez, no livro Clavis Matematicae publicado em 1631. Ainda nesse mesmo ano, Harriot, para indicar também o produto a efetuar, colocava um ponto entre os fatores. Em 1637, Descartes já se limitava a escrever os fatores justapostos, indicando, desse modo abreviado, um produto qualquer. Na obra de Leibniz escontra-se o sinal 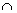para indicar multiplicação: esse mesmo símbolo colocado de modo inverso indicava a divisão.

    O ponto foi introduzido como um símbolo para a multiplicação por G. W. Leibniz. Julho em 29, 1698, escreveu em uma carta a John Bernoulli: "eu não gosto de X como um símbolo para a multiplicação, porque é confundida facilmente com x; freqüentemente eu relaciono o produto entre duas quantidades por um ponto . Daí, ao designar a relação uso não um ponto mas dois pontos, que eu uso também para a divisão."
As formas a/b e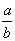 , indicando a divisão de a por b, são atribuídas aos árabes: Oughtred, e, 1631, colocava um ponto entre o dividendo o divisor. A razão entre duas quantidades é indicada pelo sinal :, que apareceu em 1657 numa obra de Oughtred. O sinal ÷, segundo Rouse Ball, resultou de uma combinação de dois sinais existentes - e :

   

Quadrados perfeitos e suas raízes

  Os pares de quadrados perfeitos:
144 e 441, 169 e 961, 14884 e 48841
e suas respectivas raízes:
12 e 21, 13 e 31, 122 e 221, são formados pelos mesmos algarismos, porém escritos em ordem inversa.
O matemático Thébault investigou os pares que têm esta curiosa propiedade. Encontrou, por exemplo, a seguinte dupla:
1113² = 1.238.769   e   3111² = 9.678.321

Alguns lugares geométricos são bem conhecidos

circunferência : lugar geométrico dos pontos de um plano que são eqüidistantes de um ponto dado chamado centro da circunferência - a distância constante é a medida do raio;

mediatriz: lugar geométrico dos pontos do plano que são eqüidistantes dos extremos de um segmento;

r: reta mediatriz do segmento - conforme a definição, r deve passar pelo ponto médio de de modo perpendicular a ele (fig. 1): essas são as propriedades desse lugar geométrico;

bissetriz interna de um ângulo: lugar geométrico dos pontos do plano que são eqüidistantes em relação aos lados do ângulo.

Você é capaz de somar os algarismos de 1 a 100 em poucos minutos?

    Carl Friedrich Gauss (1777-1855) aos 10 anos de idade respondeu rapidamente 5.050 ao seu professor  surpreendendo-o pela sua grande habilidade na matemática. Em 1792, seu talento foi reconhecido pelo duque de Braunschweig, que lhe garantiu recursos para prosseguir o estudo de matemática. Gauss criou a geometria diferencial, e fez novas descobertas como a Lei da Reciprocidade Quadrática, que introduz o conceito de congruência e o Teorema Fundamental da Álgebra. Em 1801, publicou Disquisitiones Arithmeticae, seu tratado sobre a Teoria dos Números. No mesmo ano, calculou a órbita do asteróide Ceres. Com base em uma teoria que desenvolveu, previu corretamente onde e quando o Ceres deveria reaparecer. Morreu em 23 de fevereiro de 1855, sendo considerado o "Príncipe da Matemática".
Vejam abaixo a resolução proposta por Gauss
(isso aos 10 anos de idade):

Outra forma de calcular potencias .

	Pitágoras descobriu que existe outra forma de calcular potências: através da soma de números ímpares. Ele descobriu que n2 é igual a soma dos n primeiros números naturais ímpares. Exemplo: 52 = 1+3+5+7+9 = 25

Cinco marinheiros se colocam lado a lado para receber as ordens do comandante do navio. Tente nomeá-los, da esquerda para a direita, de acordo com as informações:

• Anderson está entre Jorge e Cláudio;
• Humberto está à esquerda de Cláudio;
• Jorge não está ao lado de Humberto;
• Humberto não está ao lado de Rafael.

Obs.: Atenção! A sua esquerda não é a esquerda dos marinheiros.